La déclinaison magnétique : ce qu’il faut savoir
Je vais commencer par une petite énigme :
Imaginez que vous êtes en train de faire un trek en Nouvelle-Zélande (oui ça fait rêver !). Tout va bien, vous suivez un chemin tranquillement et vous savez même où vous êtes sur la carte. Le problème est que vous arrivez dans un endroit où vous ne voyez plus où va le chemin. Mais pas de panique, vous avez une boussole – et en plus vous êtes un lecteur fidèle de Randonner Malin. 😉
Vous prenez un azimut en direction d’un refuge qui n’est pas très loin (si vous ne savez pas ce qu’est un azimut, je vous conseille de commencer par regarder cette vidéo). Vous marchez, vous marchez, mais vous ne tombez pas sur le refuge. Qu’est ce qui a bien pu se passer ?
Oui, le refuge existe toujours.
Oui, vous avez bien lu la carte.
Oui, votre manipulation pour prendre l’azimut est correcte – à un détail près : Avez-vous pris en compte la déclinaison magnétique dans la mesure de votre azimut?
Un détail important, car c’est à cause de cela que vous êtes perdus – et nous allons voir ce que c’est.
Un nord, deux nords, trois nords ?
Vous savez sûrement qu’il existe deux nords : le nord magnétique et le nord géographique. En fait, on considère même qu’il en existe trois, mais je vous parlerai du troisième un autre jour.
Le nord géographique correspond au pôle nord, qui est l’un des deux points par lesquels passe l’axe de rotation de la Terre. Il correspond aussi à l’un des deux points où se rejoignent les méridiens.
Le nord magnétique correspond à l’un des deux points par lesquels passe l’axe du champ magnétique terrestre. Il se déplace au cours du temps à une vitesse de 60 km par an environ actuellement.
Ce qu’il faut retenir :
- Le nord géographique correspond la plupart du temps au haut des cartes topographiques. C’est le cas pour les cartes de l’IGN (Institut National Géographique) très utilisées en France.
- Le nord magnétique est le nord indiqué par l’aiguille aimantée d’une boussole.
- Le nord indiqué par le haut de votre carte n’est pas le même que le nord indiqué par l’aiguille aimantée de votre boussole. Et c’est un problème pour s’orienter ! Nous verrons pourquoi dans un instant.
La déclinaison magnétique, qu’est-ce que c’est ?
La déclinaison magnétique est l’angle (noté δ ou d) entre la direction du nord magnétique (Nm) et la direction du nord géographique (Ng). Elle est différente suivant votre localisation sur la Terre.
La déclinaison magnétique peut être positive – Nord magnétique à l’est du Nord géographique – ou négative – Nord magnétique à l’ouest du Nord géographique – (voir le schéma ci-dessus).
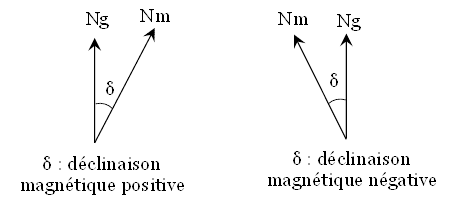
Elle est parfois exprimée en degrés, minutes d’arc, secondes d’arc – soit 3˚12’05” par exemple – ou en grades – 28 gr. Il est important de maitriser ces unités d’angle, donc voici quelques rappels :
Un degré équivaut à 60 minutes d’arc, soit 1˚ = 60’- Une minute d’arc équivaut à 60 secondes d’arc, donc 1˚ = 60’ = 3600”
- Un grade équivaut à 0,9 degré
Un degré équivaut à 60 minutes d’arc, soit 1˚ = 60’La déclinaison magnétique est généralement indiquée dans la marge des cartes topographiques à l’aide d’un petit schéma similaire à celui ci-contre.
Attention : la déclinaison magnétique n’est pas la même sur toutes les cartes car elle dépend d’où vous vous trouvez. Elle change également avec le temps – le nord magnétique se déplaçant continuellement.
Comment connaître la déclinaison magnétique à un certain endroit et une certaine date ?
Calculateur sur internet
Si vous vous y prenez à l’avance, vous pouvez calculer la déclinaison magnétique en utilisant des outils disponibles sur internet. Voici un très bon calculateur de déclinaison magnétique. Il est en anglais mais simple à utiliser même si vous ne parlez pas anglais : https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtml#declination
Il suffit de rentrer la latitude et la longitude de l’endroit qui vous intéresse ou le pays (country) et la ville (city). Vous choisissez ensuite la date, avec l’année (year), le mois (month) et le jour (day). Vous cliquez ensuite sur « calculate » et vous obtenez dans une petite fenêtre une carte, avec un dessin représentant la déclinaison magnétique et sa valeur donnée en degrés, minutes, secondes sous « declination ». Le changement par année est même donné (changing by x’ per year).
Données des cartes topographiques
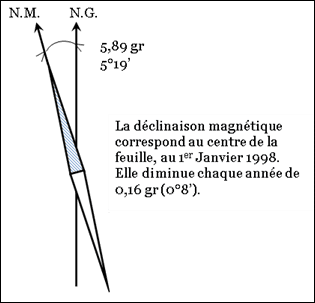
Il est aussi possible de calculer la déclinaison magnétique à la date qui vous intéresse à partir des données de déclinaisons magnétiques que vous trouvez sur une carte topographique. Voici comment faire en reprenant l’exemple du schéma précédent :
- Déterminez le nombre d’années de différence entre la date de référence donnée sur la carte et la date qui vous intéresse. Par exemple, la déclinaison magnétique de la carte est valable pour le 1er janvier 1998 et vous comptez faire votre randonnée en mars 2012. Cela fait 14 ans et 3 mois de différence, soit 14,25 ans.
- D’après les informations sur le même schéma, la déclinaison magnétique diminue chaque année de 0,16 gr, soit 0°8’. En 14,25 ans, cela fait donc un total de 2,28 gr ou 1°54’.
- Ainsi au 1er Janvier 1998, la déclinaison magnétique était de 5,89 gr ou 5°19’. Au 1er Mars 2012 cette déclinaison magnétique est donc passée à 3,61 gr ou 3°25’. La déclinaison magnétique étant négative, il suffit de soustraire 2,28 gr à 5,89 gr, de même pour un angle en degrés.
Les deux nords ne sont pas au même endroit, il y a une déclinaison magnétique, mais en quoi est-ce un problème ?
Imaginez que vous êtes au point A du schéma ci-contre et que vous voulez aller au point B à l’aide d’une carte et d’une boussole (comme je le montre dans cette vidéo). Vous prenez donc un azimut et vous savez qu’il vous faut marcher 1 km pour atteindre le point B (vous l’avez mesuré sur la carte). Si vous ne tenez pas compte de la déclinaison magnétique, et que vous marchez pendant 1 km, vous vous retrouverez au point C.
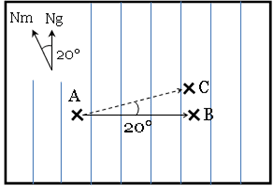
Si la déclinaison magnétique est de 20°, vous ferez une erreur de 347 m (qui correspond à la distance entre B et C).
Si la déclinaison magnétique est de 2°, vous ferez une erreur de 35 m (qui correspond à la distance entre B et C).
Donc, plus la déclinaison magnétique est importante, plus vous vous retrouverez loin du point B. De même, plus la distance parcourue est longue, plus l’erreur sera grande. Par exemple, si vous parcourez 2 km, l’erreur sera deux fois plus grande (694 m avec une déclinaison magnétique de 20° et 70 m avec une déclinaison magnétique de 2°). Si vous parcourez 10 km, l’erreur sera dix fois plus grande, etc.
Une bonne nouvelle… pour certaines personnes
En France et dans les pays frontaliers, la déclinaison magnétique est actuellement assez faible. Comme en randonnée, nous ne marchons pas en suivant un azimut pendant de très longues distances, cela n’affecte que peu la précision de nos visées. De plus, il y a toujours une marge d’erreur due à la précision de la boussole et de la lecture faite par l’utilisateur. C’est pourquoi je considère (et suis loin d’être le seul) que pour la randonnée en France et dans les pays frontaliers à l’heure actuelle, on peut négliger la déclinaison magnétique.
Une mauvaise pour d’autres…
Par contre, il y a beaucoup d’endroits où il est indispensable de prendre en compte la déclinaison magnétique. Je pense par exemple au Canada ou à la Nouvelle-Zélande où la déclinaison dépasse 20° par endroits. Donc renseignez-vous toujours avant de partir sur la déclinaison magnétique aux endroits où vous comptez randonner. Vous pouvez par exemple utiliser le site internet que je donne plus haut.
Comment corriger l’erreur ?
A quoi bon avoir une boussole si au final on ne peut pas lui faire confiance ? Rassurez-vous, il est assez facile de corriger l’erreur et de prendre en compte la déclinaison magnétique. Voici plusieurs manières de faire cela.
Avoir une boussole de pro
Certaines boussoles de qualité ont un système de correction de la déclinaison magnétique. Il suffit d’ajuster la valeur de la déclinaison magnétique à l’aide d’une vis. Une fois que cela est fait, il suffit de se servir de la boussole comme s’il n’y avait pas de déclinaison. Les autres méthodes sont faites pour les personnes qui n’ont pas ce type de boussole.
Cartes orientées vers le nord magnétique
Le haut de certaines cartes topographiques ainsi que les lignes verticales tracées sur ces cartes pointent vers le nord magnétique. Dans ce cas-là, c’est très simple, il suffit de prendre ses azimuts en se servant de ces lignes. Elles ne sont pas très courantes, mais j’ai déjà vu de telles cartes pour des courses d’orientation en Australie par exemple.
Correction manuelle
Une fois que vous connaissez la valeur de la déclinaison magnétique de l’endroit où vous êtes, vous pouvez la soustraire à toutes vos valeurs d’azimuts.
Par exemple :
- Si elle est de 8° ou 8°E (E pour Est), vous soustrayez 8° à tous vos azimuts.
- Si elle est de -11° ou 11°W (W pour Ouest), vous additionnez 11° à tous vos azimuts (vous soustrayez -11°).
Cependant, c’est une méthode que je ne vous recommande pas. Il y a des chances que vous oubliez de le faire. Il y a des chances que vous vous trompiez entre les + et les -, et qu’au lieu de corriger l’erreur, vous vous retrouviez avec 2 fois l’erreur.
Non je ne doute pas de vos facultés, je sais simplement que la fatigue, la panique ou autres peuvent nous faire faire des choses étranges. Donc autant avoir un système le plus simple possible, que voici.
Une astuce très pratique
La méthode la plus pratique et la plus simple est je pense de tracer sur votre carte des lignes parallèles au nord magnétique (en pointillés rouges sur le schéma). Faites-le pendant la préparation de votre randonnée, je doute que vous puissiez faire un travail propre et précis une fois sur le terrain.
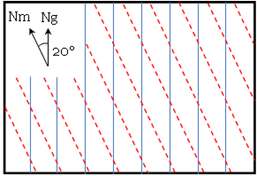
Quand vous prendrez un azimut, il vous suffira d’aligner le nord du cercle gradué de votre boussole avec le nord magnétique (le haut des lignes pointillées rouges) et non pas avec celles qui pointent vers le nord géographique (lignes bleues).
Le mot de la fin
Félicitations, vous avez tout lu ! J’espère que je suis resté assez simple dans mes explications et que vous y voyez un peu plus clair maintenant. Si vous avez des questions, n’hésitez pas à les poser dans les commentaires. Je me ferai un plaisir d’y répondre.
N’hésitez pas à partager cet article sur Facebook ou Twitter en cliquant sur les boutons juste en dessous, il pourrait intéresser un ou une de vos ami(e)s.
Intéressant.
Bonjour
Je suis en train de construire un quadrant surmonté d’un cadran qui me donne la position angulaire du soleil par exemple ! Ce dernier se révèle assez juste ! Mais le cadran révèle beaucoup d’écart environ 7 degrés entre la position réelle du soleil et celle que me donne mon logiciel !
Je viens de prendre conscience que les boussoles du commerce sont assez laxistes ! Ajoutons que mon appareil est en bois !
Ma question j’habite à Vescours dans le 01560 et j’aimerai connaître le nombres de degrés à ajouter ou retrancher à ce que je lis sur ma bousolle !
D’avance merci !
http://www.sunearthtools.com/dp/tools/pos_sun.php?lang=fr
à voir si ce site peut vous aider à répondre à votre attente
bonjour à tous.
pourquoi sur les cartes ign datant d’avant 2001 la déclinaison magnétique diminue et apres 2001 elle augmente ?
merci à tous.
Est-ce que vous parlez de la déclinaison magnétique ou de sa variation annuelle ?
bonjour françois jourjon
merci de votre correspondance
la variation annuelle de la declinaison magétique est de 0.13gr (0°7) est (géographique) depuis à peu près 2001.
avant 1999 on calculait la variation annuelle de la declinaison magnétique vers l’ouest.
regardez vos cartes c’est écrit.
je veux dire par ce fait qu’il y a eu une inversion du champ magnétique terrestre entre 1999 et 2001 et personne en parle.
Bonjour,
La variation annuelle de déclinaison magnétique n’est pas constante dans le temps et peut effectivement passer d’est à ouest ou d’ouest à est au cours du temps.
Cela ne correspond par contre pas du tout à une inversion du champ magnétique terrestre, car une boussole pointerait vers le pôle sud.
De plus, ce sont des phénomènes de grande ampleur, qui se stabilisent après une longue période (à l’échelle humaine) et ça ne passerait pas du tout inaperçu.
Bonne journée,
François
Les cours des glénans m’ont appris un truc mémotechnique pour retenir le négatif ou le positif
Est moins Ou est (Ouest) plus ?
Et encore merci pour toutes ces explications claires et précises
Le petit problème avec le truc des Glénan c’est qu’il est réversible.
J’en utilise un à mon avis plus sûr, du moins en langue française.
La déclinaison c’est un mot féminin et le symbole féminin ( miroir d’Aphrodite ) c’est un O qui surmonte une croix : O pour ouest et la croix pour + .
Pour l’ Est le E c’est un C avec un moins au millieu.
Tout comme mon homonyne, je vous dit merci; les explications claires et abordables sont rares sur le sujet.
Bonne rando
Jacques
Ou plus simplement comme on prononce naturellement Est Ouest plutot que le contraire vous pensez juste à un zero entre les deux, l’Est se trouve à gauche de zero c’est négatif, l’Ouest a droite c’est positif.
En anglais et en rime :
East is least (-), West is best (+)
😉
Pas mal. 😉
P.S. Comme très sympathiquement expliqué dans cette vidéo en anglais (Magnetic Declination Demystified)
https://www.youtube.com/watch?v=peu7uMp0cVU
il n’est même pas la peine de se souvenir de quoi que ce soit, quand on a une carte qui montre les 2 flèches :
– si le Nm est à gauche du Ng (déclinaison O), on devine intuitivement qu’il faut rajouter des d° pour compléter le cercle
– si au contraire le Nm est à droite (déclinaison E), on est « au-delà » et il faut donc soustraire des d°.
Note : si quelqu’un trouve le temps de répondre à ma question ci-dessous (28 août 2019, 18:39), je lui en serai grandement reconnaissant !
Merci François pour les explications. Serait-il possible de commander les guides concernant le matériel de randonnée par chèque et si oui, merci de me faire parvenir le bon de commande.
Bonjour Jean-Luc,
Malheureusement,ce n’est pas possible pour l’instant de commander les guides par chèque.
A bientôt,
François
c’est plutôt une question :
sur la plupart des boussoles, une graduation apparaît pour la correction du nord magnétique.
or il y a peu de discours sur le mode d’utilisation de cette graduation.
soit c’est trop simple ou trop évident pour avoir besoin d’en parler
soit personne ne souhaite en faire usage
à votre avis ?
Bonjour Jean-François,
Ces graduations peuvent être utilisées pour prendre un azimut. Au lieu d’aligner l’aiguille rouge avec la graduation correspondant au Nord, on l’aligne avec la graduation de la déclinaison magnétique correspondante.
Est-ce que c’est clair ?
A bientôt,
François
très clair
et quand même plus simple que de faire des calculs mentaux sur les azimuts, je trouve
Bonjour François
Bravo et merci pour ce site très bien fait, très intéressant et pour vos randonnées. Une petite chose concernant la déclinaison magnétique : il ne vaut mieux pas se servir du quadrillage bleu sur les cartes IGN pour obtenir le Nord Géographique, en effet c’est le quadrillage UTM (pour les coordonnées GPS) et ce quadrillage n’indique pas du tout le Nord Géographique, il faut prendre les lignes noires (les méridiens) ou le bord de la carte (voir le sens des écritures) pour avoir le Nord Géographique. Certe les méridiens sont assez espacés, il suffit d’en retracer avant de partir ! Cordialement
Olivier
Bonjour Olivier,
Merci pour votre commentaire très juste. J’avais choisi le bleu pour mon illustration sans penser que cela pouvait prêter à confusion.
A bientôt,
François
Bonjour Olivier,
Bonjour François,
Je me permets d’intervenir car je reste étonné de la manière dont on gère la déclinaison magnétique, il est vrai qu’en France métropolitaine, elle est si faible qu’on a rarement besoin d’en tenir compte dans la pratique habituelle de la randonnée pédestre.
Il en va différemment quand on part dans un coin ou ça ne peut plus être négligé. Je me suis déjà étonné de ce que les fabricants de boussoles gravent sur le fond des boussoles une échelle magnétique et que rarement quelqu’un parle de l’utiliser tout simplement.
Si on n’a pas la chance d’avoir une boussole qui a prévu un réglage du repère nord magnétique, et pour rendre les choses encore plus pratiques, on peut faire marque avec un stylo tipex, vérifiez d’abord si c’est possible de gratter la gouache de correction sans laisser le trace. Ensuite il faut tenir compte de l’épaisseur de l’aiguille, et envisager plutôt 2 points de part et d’autre de celle-ci.
Ainsi il est possible de ne pas surcharger la carte, et d’ailleurs en cas de réutilisation plusieurs années après, la déclinaison aura changé, que faire alors ? Racheter une carte ?
Pour se caler sur le quadrillage UTM, n’étant pas localement aligné sur le nord géographique, il suffit de dessiner le nord géographique à coté avec un rapporteur et de relever le résultat par rapport à UTM.
Le modèle magnétique étant basé sur un très grand nombre de stations de mesure, et de relevés satellite, et d’un modèle mathématique pour approcher ces résultats, la valeur en un lieu est obtenue par interpolation, il y a naturellement un grand nombre de décimales, je pense qu’il faut retenir la valeur arrondie à 2° près pour utilisation sur le terrain, la boussole et les yeux ne sont pas adéquats pour gérer une meilleure précision.
Bonnes randos
Bonjour Jean-François,
Effectivement, les échelles fixes de déclinaison magnétique sont pratiques. Mais, il est facile d’oublier de faire la correction. Je ne connaissais pas l’astuce du tipex, je la trouve très intéressante – c’est une très bonne idée !
Effectivement, les traits sur la carte, ce n’est pas l’idéal une fois que a déclinaison a changé. Il est possible de les faire au crayon à papier, mais le gommage est délicat.
Merci pour ton commentaire et à bientôt,
François
Bonjour, très bon site, une question néanmoins:
En 20 ans quelle est la position magnétique du nord de strasbourg par rapport à 1993 ?
En bref de combien à t il bougé ?Et c’est bien vers l’est qu’il à bougé si j’ai bien compris?
Merci de votre aide !
Amicalement,
Lucas.
1993-04-23 0° 50′ 8″ W changing by 6.0′ E per year
2014-04-23 1° 37′ 31″ E changing by 7.8′ E per year
par utilisation de la calculette de la nasa
Merci de la rapidité de cette réponse !
Amicalement,
Lucas.
petite question concernant la déclinaison de ton exemple
je n’arrive pas a comprendre comment vous trouver la valeur en degré, minute, seconde de 2,28grade.
en effet pour moi ca fait loin les cours de maths.
autrement serait il possible de connaitre la déclinaison magnétique a partir de chez moi pour le mois de mai 2013
je suis de Sierentz dans le Haut-Rhin
d’avance merci
Philippe
Bonjour Philippe,
Elle est d’environ 1,5° E au mois de mai. Sur des distances courtes en randonnée, tu peux la négliger.
A bientôt,
François
merci beaucoup pour la réponse pourrais je te demander comment tu la calculée
merci
Philippe
r
J’ai utilisé le calculateur que j’indique dans l’article.
ben oui c’est évident
encore merci
Salut il faut faire une conversion.pour passer de grade en degré.
100grade =90degre
2,,28grade=. ?
Il faut faire la règle de trois
sinon dans ton exemple j’arrive a trouver la déclinaison en grade en faisant 0,16X14,25 mais je n’arrive pas a trouver cette même déclinaison en degré peux tu m’expliquer
Philippe
Il faut penser que c’est une base de 60.
14,25 x 8′ = 114 ‘
Comme 60′ = 1°
Cela donne 1°54’
ok ca a l’air tellement simple
merci et la c’est fini je t’embête plus ce soir
bonne soirée
Bonjour Philippe
Tu fais bien de poser la question car en voulant faire une vérification, par simple curiosité, j’ai trouvé une différence par rapport aux résultat attendu.
Essayons un petit retour sur les fondamentaux:
400gr = 360° soit 1gr = 360/400 = 0,9°
2,28gr x 0,9 = 2,052° = 2° + 0,052°
1° = 60′ soit 0,052 x 60 = 3,12′ = 3′ + 0,12′
1′ = 60 » soit 0,12 x 60 = 7,2 »
D’où 2,28gr = 2°3’7,2 »
Question: pourquoi cette différence par rapport au résultat présenté de 1°54′ ?
A propos de la déclinaison, on lit sur la carte: «Elle diminue chaque année de 0,16gr (0°8′)»
Cette valeur de conversion 0°8′ est en fait arrondie par défaut.
En effet :
0,16gr x 0,9 = 0,144°
Soit en minutes 0,144 x 60 = 8,64′ = 8′ + 0,64′
0,64 x 60 = 38,4 »
D’où 0,16gr = 0°8’38,4 »
En fait, c’est l’arrondi par défaut affiché sur la carte qui fait la différence.
En effet on a bien 0,144° x 14,25 = 2,052° = 2°3’7,2 » = 2,28gr
Cordialement
Bernard77400
Suite et fin.
La différence entre les deux résultats est de 2°3’7,2 »- 1°54′ = 0°9’7,2 ».
Autant pour la précision d’un tir, ainsi qu’en astronomie une valeur aussi faible a toute son importance, il n’en est heureusement pas de même en randonnée pédestre où cela n’a aucune incidence quant à l’orientation. D’ailleurs, si on prend seulement en considération l’arrondi des deux résultats obtenus on retient 2° dans les deux cas, valeur par excès pour 1°54′, par défaut pour 2°3’7,2 ».
Histoire de pousser le luxe du détail, on peut même calculer l’écart de position provoqué par cette différence de 00°09’07 » entre les deux résultats.
Cela revient à calculer la longueur de la corde sous-tendue par un angle de cette dimension placé au centre d’un cercle.
l/2 = r sin (Ô/2)
avec:
l = longueur de la corde = écart de position
r = rayon du cercle = distance de la position à vol d’oiseau
Ô = Angle au centre = différence entre les résultats
soit pour une distance de la position de 10 km = 10 000 m:
l /2 = 10 000 sin (00° 09′ 07 »/2) = 7,915
l = 7,915 x 2 = 15,83
D’où un écart de position de 15,83 m à une distance de 10 km à vol d’oiseau.
Merci pour ces petits calculs. En tout cas, ça permet bien de vérifier que les arrondis utilisés n’ont pas d’impact sur la précision que l’on a en randonnée. 😉
Tout à fait d’accord.
A tel point que par analogie avec cette citation de Descartes:
«la géométrie est l’art de raisonner juste sur des figures fausses»,
jusqu’à une certaine limite, on pourrait presque dire que
«la navigation est l’art d’arriver juste avec des mesures fausses»
déjà : Bonne année à François et Bernard,
au lieu de trainer toutes ces décimales :
« l’arrondi de la somme est égal à la somme des arrondis »
voilà ce que je dirais
ceci est probablement du au fait que la somme est une opération régulière dans l’espace considéré : les nombres relatifs décimaux.
mais je suppose qu’un prof de maths dirait ça beaucoup mieux
autrement, tout à fait d’accord avec Bernard, quand on fait une approximation sur le terrain, autant savoir l’écart que l’on risque de faire.
Je maintiens qu’on peux s’en sortir sur le terrain sans faire de calculs, c’est au moins le truc pour ne pas faire d’erreur.
Bonjour Jean-François
Je suis bien d’accord, sur le terrain il est tout à fait préférable de ne pas avoir à réaliser des calculs, surtout quand on n’est pas sûr de son affaire. Tout comme toi, je pense qu’il vaut mieux user d’un artifice matériel plutôt que de se tromper. Toutefois quand cela s’avère indispensable, de préférence au cours de la préparation, il me semble important de maîtriser le sujet et de bien vérifier les résultats pour ne pas s’embarquer dans une aventure avec des erreurs qui pourraient avoir des conséquences plus ou moins désagréables.
Voici les règles que j’applique pour les petits calculs scientifiques et techniques:
. pour obtenir un maximum de précision, j’effectue les calculs avec un maximum de chiffres manipulables après la virgule;
. sauf cas particulier, la somme des nombres arrondis n’est pas égale à l’arrondi de la somme de ces nombres, aussi c’est uniquement le résultat que j’arrondis selon l’approximation acceptée;
. si le chiffre considéré est égal ou supérieur à 5, j’arrondis par excès le nombre au chiffre immédiatement supérieur. S’il est inférieur à 5 j’arrondis par défaut le nombre en supprimant ce chiffre, ainsi que tous ceux positionnés à sa droite.
Éventuellement je peux être amené à tronquer le résultat pour ne retenir que les chiffres significatifs qui m’intéressent, sans autre considération. Par exemple au sujet de la déclinaison magnétique précédente chiffrée à 8′, en toute rigueur j’aurais dû écrire «tronquée à l’unité» à la place de «arrondie par défaut» (je n’ai pas pu corriger car une fois envoyé, le texte n’est malheureusement plus accessible pour modification). En effet, selon l’application stricte de la règle précédente l’arrondi par défaut de 8,64′ ne peut être que 8,6′ tandis que l’arrondi par excès à l’unité est 9′, à l’évidence plus proche du résultat calculé que la valeur tronquée qui a été retenue. Je suppose que ce choix relève d’un critère autre que la précision du calcul.
Effectivement, comme tu le soulignes, il est intéressant de connaître l’implication de l’approximation d’une mesure effectuée, en particulier lorsque l’on est en action sur le terrain.
En utilisant le modèle précédent, je peux facilement calculer quelle est la longueur du segment sous-tendu par un angle de 1° à une distance à vol d’oiseau de 1 km = 1000 m.
l = 2 d sin (Â/2)
avec:
l = longueur du segment
d = distance de la position à vol d’oiseau
 = angle de 1°
l = 2 x 1000 x sin (1°/2) = 17,45 m
Soit un segment d’environ 17 m de longueur par degré d’angle de la boussole et par kilomètre de distance à vol d’oiseau. Ainsi, il suffit de multiplier ce résultat par le nombre de degrés et/ou de kilomètres pour l’adapter aux circonstances.
Bonne année 2014
Bernard77400
Suite et fin….
L’approximation de la longueur d’un nouveau segment obtenue en multipliant directement par un angle différent le résultat calculé pour 1° n’est bien sûr valable que pour de faibles valeurs angulaires, sinon il faut recalculer le sinus, ce qui nécessite de disposer d’une calculatrice scientifique sur le terrain.
Cela correspond généralement à des erreurs de mesure induites par:
. une déclinaison magnétique faible non prise en compte;
. un réglage d’azimut approximatif du cadran de la boussole;
. une visée peu précise pour le relèvement de l’azimut d’un repère.
Exemples de calculs pour  = 5° et d = 5 km
Calcul approché de la longueur du segment:
l1 = 17,45 x 5 x 5 = 436,25 m
Calcul complet de la longueur du segment
l2 = 2 x 5000 x sin (5/2) = 436,19 m
bonjour
moi je sui un nauvice sur la topographie militaire , je voudrais que vous puissiez maider a mieu comprendre daventage la topographie du debut merci
Bonjour,
Je vous félicite pour la clarté de l’explication de la déclinaison magnétique.
Au début de cette explication, vous évoqué un troisième nord. Quel est-il ?
Recevez mes meilleures salutations.
Marc Tisserand
Bonjour Marc,
Le troisième nord est le nord du quadrillage qui est présent sur certaines cartes. Par exemple, sur les cartes IGN « compatibles GPS », il y a un quadrillage kilométrique UTM qui est représenté en bleu. Le troisième nord est la direction des lignes verticales de ce quadrillage (en allant vers le haut).
A bientôt,
François
Bonjour,
Je vous remercie pour votre réponse très claire.
Recevez mes meilleures salutations.
Marc Tisserand
Pour ceux d’entre vous qui préférez un site français, il y a aussi un calculateur de déclinaison à cette adresse.
http://www.geomag.nrcan.gc.ca/calc/mdcal-fra.php
Salutations!
Bonjour Denis,
le problème n’est pas forcément la langue, si toutefois c’est de l’anglais …, mais surtout qu’il y ait toutes facilités pour alimenter les coordonnées de la région qui intéresse, malheureusement le site canadien ne fournit pas d’aide pour cela.
http://www.ngdc.noaa.gov/geomag-web/#declination
est présenté à coté d’un accessoire permettant de déterminer les coordonnées : sélection d’un pays, et dans ce pays, une des principales villes, les chiffres de la longitude et la latitude sont alimentés au bon endroit. Fournir aussi la date du futur voyage. Le résultat s’affiche sur un petit bout de carte, montrant la rose des vents basculée vers le nord magnétique, et la déclinaison en degrés (décimaux). La variation annuelle est également indiquée, mais attention ce sont des minutes décimales.
Cas du smartphone : le calculateur invoqué à partir d’un smartphone android (à vérifier pour les I-Phones), la position de celui-ci est utilisée, ainsi que la date du jour, la carte s’affiche avec la rose des vents basculée vers le nord magnétique. La déclinaison est aussi fournie en chiffres, c’est utile pour ceux qui ont oublié de s’informer avant.
autre calculateur encore plus pratique (merci les Anglais) : World Magnetic Model 2010 Calculator
http://www.geomag.bgs.ac.uk/data_service/models_compass/wmm_calc.html
un simple clic sur la carte du monde zoomable donnera toutes les infos. Important : le point peut être mémorisé, afin de comparer avec un autre, mémorisable à son tour, exemple: comparer la déclinaison entre 2 points de la France, Le Finistère et la Corse.
encore un autre calculateur : aller voir dans la page le paragraphe :
A Javascript implementation of the World Magnetic Model
http://www.bdcc.co.uk/Gmaps/Services.htm
enfin
http://magnetic-declination.com/
(semble utiliser un modèle de données périmées, à surveiller)
bonnes randos (n’importe ou dans le monde)
Bonjour,
je me pose une question concernant la valeur positive ou négative qu’on attribue à l’EST ou à l’OUEST afin de corriger la déclinaison magnétique EST + et OUEST – . C’est la formule donnée dans un livre d’instructions sur l’utilisation d’une boussole venant de la France, puis ça me semble le contraire pour la formule suggérée pour l’utilisation d’une boussole au Canada. Si j’ai bien compris contrairement à l’Europe au la France au Canada on additionne pour corriger la déclinaison OUEST alors qu’en France on le soustrait puis c’est le contraire pour la valeur de la déclinaison EST qu’on additionne en France alors qu’on le soustrait au Canada .
Merci de me donner l’explication ou si j’ai tout simplement mal interprété ma lecture.
Bonne journée
JPC
Bonne journée
JPC
http://geomag.nrcan.gc.ca/mag_fld/compass-fra.php
Bonjour Jean-Pierre
si j’en crois les explications données par le site « officiel » du Canada sur la déclinaison magnétique et l’utilisation de la boussole, je pense qu’il n’y a pas de différence, le cap progresse dans le sens positif comme les aiguilles d’un montre.
De fait une correction vers l’est est notée + (plus)
par symétrie vers l’ouest, c’est noté – (moins)
Je pense que le plus simple pour ne pas se tromper est de faire un petit schéma avec le nord géographique et le nord magnétique et de faire une vérification rapide (à l’azimut 0°) une fois que l’on a corrigé sa boussole (ou sa carte) pour prendre en compte la déclinaison magnétique.
Bonjour.
Tout d’abord merci pour ces explications simples et à la fois complètes pour démarrer un parcours d’un point à l’autre. Je ne m’attache pas pour le moment à rectifier les erreurs d’un point A sur B dûes à la déclinaison entre le NM et NG. Ce sera pour plus tard. J’ai commandé cette boussole et pense avoir fait le bon choix??? >> Recta DS-50 Global-System Boussole (tu peux m’en dire quelques mots?) Je l’attends ce mardi.
Mon site n’a rien à voir ici quoique les oiseaux (pigeons par ex) arrivent à se repérer dans leur vol pour retrouver le chemin du bercail ; ce serait intéressant de comprendre. A bientôt sur ton site.
Bonjour Christophe,
Cette boussole est très bien pour s’orienter en randonnée. En plus, avec le système global, tu peux aller partout dans le monde sans problème : attention à bien corriger la déclinaison magnétique par contre.
A bientôt,
François
Bonjour,
quelle est l’orientation du quadrillage bleu sur les cartes IGN serie Bleu au 25000.
Si j’oriente ma carte en prenant ce quadrillage en référence, existe t – il des corrections à appliquer.
Ce quadrillage démarre vers l’Est et l’Ouest à partir du méridien central du fuseau. Sur les cartes près de ce fuseau est ce que ce quadrillage est = au nord géographique.
Correction: Sur les cartes près de ce méridien est ce que ce quadrillage est = au nord géographique.
Bonjour Romain,
Le quadrillage bleu (quadrillage UTM) n’est ni orienté vers le nord géographique, ni vers le nord magnétique. Les corrections à appliquer ne se déterminent pas facilement avec la carte entre les mains. C’est pour cela qu’il vaut mieux ne pas se servir de ce quadrillage avec la boussole.
Par contre, les méridiens tracés (en degrés ou en grades) indiquent la direction du nord géographique. Souvent d’ailleurs, les bords verticaux des cartes IGN correspondent à des méridiens (même si c’est en train de changer avec la nouvelle édition).
A bientôt,
François
Merci François pour tes explications.,
Romain
merci bien
veuillez nous expliquer la « lévitation magnétique Mr Francois
J’ai un nouveau gps portable que j’utilise pour la pêche, et je ne sais quel nord adopter (car on doit configurer le gps et j’ai le choix entre le nord magnétique et le vrai nord). Quelqu’un peut-il me dire si les coordonnées d’un waypoint que j’entre dans le gps changent si je change de nord?
RMgps141129_1719
Bonjour raadfisher,
Le réglage « Nord magnétique » s’utilise pour connaître l’azimut par rapport au Nord magnétique, par exemple pour régler un azimut sur une boussole-rapporteur.
Le réglage « Nord vrai » s’utilise pour connaître l’azimut par rapport au Nord vrai ou Nord carte, par exemple pour tracer un azimut sur une carte papier.
« Quelqu’un peut-il me dire si les coordonnées d’un waypoint que j’entre dans le GPS changent si je change de nord? »
Pour connaître la réponse il suffit de faire une manip toute simple sur ton propre GPS.
Cordialement,
Bernard77400
Merci pour ta réponse, tu m’as devancé. 😉
Bonjour pêcheur,
à la question :
Quelqu’un peut-il me dire si les coordonnées d’un waypoint que j’entre dans le gps changent si je change de nord?
le choix du nord (magnétique / géographique) ne change pas les coordonnées.
Déclinaison magnétique et GPS.
Un GPS ne relève pas de caps, mais des coordonnées de points, si le terminal est stationnaire, il indique le point, sans pouvoir orienter le fond de carte par rapport au boitier.
(ici on ne parle pas des GPS de marine à 2 ou 3 antennes, n’ayant plus besoin de mouvement pour s’orienter)
Si le terminal est en mouvement, il est capable d’orienter le fond de carte correctement par rapport à ce mouvement, alors il se réfère au Nord Géographique, s’il indique le cap de la progression. Le terminal peut présenter le fond de carte avec la direction du mouvement en haut, ou bien le Nord (géographique) en haut.
Les terminaux intègrent parfois un capteur magnétique, selon une tendance qui remonte à l’époque ou la précision du GPS était dégradée volontairement par les militaires, la détermination du Nord manquait alors de précision. La faible différence de coût incite à continuer d’acheter ces appareils, il est à noter que certains téléphones, mais surtout les smartphones intègrent un capteur magnétique 3 axes.
Important : un appareil avec un capteur magnétique doit être recalibré à chaque démarrage à froid (changement de batterie, période d’inutilisation), suivant la procédure indiquée par l’appareil (2 tours, ou un huit), et qui a pour but de distinguer les champs parasites du champ terrestre, faute de quoi l’indication est fantaisiste.
L’utilisateur peut configurer son appareil pour que la boussole électronique présente soit :
le nord magnétique, le nord géographique (en plus gérer une bascule de l’un vers l’autre en fonction de la vitesse du mouvement, le nord magnétique étant prioritaire à l’arrêt, ou aux basses vitesses), le nord de la grille (certaines cartes n’ont pas le nord géographique exactement en haut), ou enfin, un angle déterminé par l’usager (on imagine la déclinaison officielle de l’endroit concerné).
Cela dit, à mon point de vue le terminal est surtout utile pour vérifier une trace (une suite de points), et pour l’enregistrer. S’il présente aussi un fond de carte (zoomable) c’est bien, mais attention à l’arrêt, l’orientation du fond ne doit pas être pris en compte.
Merci beaucoup pour votre disponibilité, Bernard, François, Jean François… Les réponses ainsi que le site m’en apprennent….
Raad
Bonjour Raad,
Confucius:
« J’entends, j’oublie. Je vois, je me souviens. Je fais, je comprends. »
Benjamin Franklin:
« Tu me dis, j’oublie. Tu m’enseignes, je me souviens. Tu m’impliques, j’apprends. »
As-tu fait la manip sur ton GPS?
Cordialement,
Bernard77400
Excellentes ces citations, je ne les connaissais pas. 😉
Mais plus probablement connais-tu ce proverbe chinois:
« Si tu vois un homme qui a faim, donne-lui un poisson tu le nourriras pour un jour. Apprends-lui à pêcher et il se nourrira toute sa vie. »
Oui tout à fait !
BOnjour J’aimerais connaître le point terrestre où l’inclinaison magnétique est de 60° Merci
Inclinaison ou déclinaison magnétique ?
Je n’ai pas encore eu le temps d’aller en mer pour essayer le nouveau gps, de plus la météo ne m’en a pas donné l’occasion. Je ne manquerai pas de vous transmettre mes constatations.
Raad.
Je reste en attente des conclusions de l’essai d’un GPS en mer …
Le manque d’éléments de comparaison m’interpelle.
Bjr mon ami je suis au Niger. veuillez m’aider avec des exercices à traiter sur la déclinaison magnétique ou bien en général sur les directions de référence. j’attends incessamment. Merci d’avance.
Additif: Et sur les unités de mesure d’angle.
additif, Et sur les unités de mesure d’angle.
J’aime aussi la randonnée et je veux apprendre à m’orienter mieux.Mais les personnes qui interviennent ici ,je me pose la question:ce sont des cracks ou des vantards?
J’aimerais échanger avec des personnes comme moi….qui ne prennent pas l’avion pour randonner.Je marche même en ville et dans les faubourgs ,les forêts périurbaines.
Quand je lis ce qu’écrivent toutes ces personnes,je n’ai plus envie de voyager,ça me coupe mes rêves.
Je ne peux pas répondre pour les autres, mais je pense ne faire partie d’aucune des 2 catégories.
Salut ! Ton (permets moi de te tutoyer) site est très intéressant. Je me suis retrouvée dessus suite à la question d’un jeune (13 ans) qui voulait connaître le calcul entre nord géographique et nord magnétique. Ca m’amène à une question : comment l’expliquer simplement ?
Merci d’avance si tu réponds avant ce soir, et merci dans tous les cas 🙂
Alizée
Ps : nous sommes en colo de Course d’Orientation donc nous avons l’habitude d’utiliser la boussole etc…
Bonjour,
Le plus simple est d’avoir un dessin du globe avec le nord géographique et le nord magnétique et de regarder les différences d’angles entre une position sur la Terre et une autre.
À bientôt,
François
Bonjour,
Je découvre ton site qui est très complet et intéressant, de plus ta méthode pédagogique fonctionne vraiment bien. Ma question porte sur du matériel :
J’ai l’opportunité en équipement d’avoir :
*un « ancien » altimètre Altiplus N1 Pretel (made in France)
*une boussole Breithaupt avec miroir/visée et clinomètre intégré (made in Allemagne)
*une boussole Suunto KB14 et un clinomètre Suunto PM5 (made in ?)
Peux-tu m’apporter un avis, des conseils ou simplement j’utilise son iPhone (avec boussole et clinomètre)
Merci François
Bonsoir, Tout à fait excellent et clair. C’est très méthodique et progressif. Vous ne laissez rien au hasard et nus permettez d’anticiper nos erreurs. Je viens de découvrir ces derniers jours votre site et ce sera mon « livre de chevet » pour la Randonnée. Merci déjà !
Bonsoir Monsieur/Madame,
je me nomme dakouri eric,je suis ivoirien et je viens en cote d’ivoire à Abidjan.
je souhaite connaitre comment convertir des coordonnées géographiques en coordonnées cartésiens.
Exemple .
Lat (N) : 05°15’16.21 »
Long(w) : 003°55’43.16 »
Juste avoir le mode opératoire de calcul de conversion en X et Y
Merci et bonne soirée à vous.
Bonjour,
Le plus simple est d’utiliser un convertisseur comme celui-ci : http://twcc.fr/#
Bonne journée,
François
Bonjour
Néophite dans la brume
Voici un problème théorique:
Imaginons qu’en 1800, un type se trouve au point A: Lat (N) : 50°30’30″ & Long(E) : 5°30’30″
La déclinaison magnétique pour ce point était de : 21°17′ W en 1800.
– Le type localise un point B par rapport à lui au point A, se trouvant à 500 kilomètres dans un angle de 50° par rapport au pole nord magnétique.
En l’an 2000, un autre type se retrouve au point A, donc: Lat (N) : 50°30’30″ & Long(E) : 5°30’30″
La déclinaison magnétique est maintenant de : 0°58’ W en l’an 2000
Je veux retrouver le point B en sachant qu’il est donc à 500 kilomètres et à 50 degrés par rapport au pôle magnétique tel qu’établit en 1800.
Je vais donc devoir corriger l’angle étant donné que le pôle magnétique se « balade ».
Dans ce cas, je devrais calculer la différence des deux déclinaisons magnétiques et le soustraire à mon angle de 50 degrés? = 50° – 19°02″ = 30°58′ le nouvel angle.
Suis-je un explorateur perdu ou vais-je trouver le point B au terme de mes calculs?
Il y a t-il d’autres méthodes de parvenir au même résultat si il est bon évidemment?
Merci de me corriger.
Bonjour Attilio,
Peux-tu expliquer comment tu as obtenu la différence de 19°02″?
Cordialement;
bernard77400
Oui, erreur, ce serait plutôt 20°19″
Par curiosité, il peut être intéressant de calculer la distance qui sépare le point B (en 1800) du point B’ (en 2000) si l’on ne tient pas compte de la dérive de la déclinaison magnétique.
Vous m’intriguez… Pour être sur de bien comprendre, Il-y aurait-il une dérive possible du point B qui serait significative pour un temps relativement court, 200 ans.
J’imagine que ça dépend de la précision exigée.
Ça doit concerner aussi le point A.
Merci d’avance.
D’après ce que je comprends, tu dois faire allusion à la dérive des continents qui pourrait affecter les coordonnées géographiques des points A et B. Bien entendu, ce n’est pas le sujet.
Dans le cas présent, c’est simplement le déplacement du pôle Nord magnétique entre 1800 et 2000 qui nous préoccupe.
Le point B est, bien sûr, toujours à la même place qu’en 1800. C’est seulement la mesure de son azimut qui est différente du fait de la déclinaison magnétique qui n’est pas la même en 2000.
En 2000, si l’on utilise le même azimut qu’en 1800, le point B apparaîtra faussement déplacé par rapport à sa position relevée en 1800. C’est cet écart qui peut être intéressant de déterminer.
Suite du néophyte dans la brume…
J’ai oublié que quand le type de 1800 me dit que le point A est à 50°30’30″N et 5°30’30″ E,
il faut tenir compte d’abord qu’étant Français, il aurait sans doute utilisé le méridien de Paris, situé environ 2 degrés plus à l’est de celui de Greenwich devenu la norme mondiale du méridien 0 vers la fin du dix-neuvième siècle, je pense.
J’ai trouvé aussi que si je ne tenais pas compte de la déclinaison magnétique, en utilisant en l’an 2000 les données de 1800 sans correction, je me retrouverais environ à 175 kilomètres du point B.
Le méridien de Paris est effectivement décalé de 2°20’13,82″ à l’est de celui de Greenwich.
Mais, es-tu certain qu’il s’agit bien d’un Français, car le point A se situe en Belgique, et le point B en Allemagne?
Effectivement, si l’on ne tient pas compte de la dérive du pôle Nord magnétique entre 1800 et 2000, le calcul de l’erreur de la localisation du point B donne bien 175, 24 km.
Quant à mon vieux GPS12, il affiche 133° et 176 km.
Dans ce cas, aucune chance de trouver un trésor enfoui au point B en 1800!
Ton cas d’école montre bien qu’il peut être indispensable de tenir compte de la dérive du pôle Nord magnétique.
Je viens de regarder une carte de 1800 et la France était à l’époque beaucoup plus grande, 616 700 kilomètres carrées et le Rhin servait de frontière au nord est.
Suite à la révolution sanguinaire (française) qui devait remplacer un régime autocratique par un régime despotique au nom de la liberté, les frontières se sont souvent déplacés compte tenu des altercations avec les voisins royalistes, mais en 1800, la France était un grand pays qui englobait la Belgique au complet et une partie de l’Allemagne.
Donc, on peut dire que mon type en 1800 était une sorte de français amélioré, un belge devenue français. Il était général dans l’armée française et se serait embarqué dans l’expédition de Napoléon Bonaparte en Égypte.
Une fois la-bas, pressentant que ça allait mal tourner, il serait revenu assez vite avec un beau butin non déclaré.
De retour en France et pressentant aussi ce que la France allait devenir, il se serait dit que ce n’était pas un bon pays pour y enterrer un trésor.
Alors dans une de ses visions, il aurait vu un pays idéal dont le nom se terminait en « bourg » ou en « stein ». Il aurait donc décider d’enterrer le trésor au duché d’Holstein dans le nord de l’Allemagne là ou se trouverait le point B selon mes estimations, environ 50 kilomètres à l’ouest de Kiel en Allemagne. (est-ce correct?)
De toute façon, il se sera trompé un peu car sa vision de pays idéal dont le nom se terminait en « bourg » ou en « stein » correspondait en fait au Luxembourg et au Liechtenstein, paradis fiscaux confirmé au XXiiéme siécle.
Quand j’ai mentionné un trésor enfoui, pour moi, c’était une boutade.
D’après ce que tu relates, il semble bien que ton problème ne soit pas un simple cas d’école pour travailler sur la déclinaison magnétique, mais bien la recherche d’un trésor historique.
Je ne dispose pas d’une carte de France de 1800, mais je peux t’indiquer les adresses actuelles proches des points A et B, en prenant le méridien de Greenwitch comme longitude 0.
Point A (WGS84: 50.50833°N, 5.50833°E):
Lagrange 16-36
Anthisnes, 4160
Belgique
Point B (WGS84: 54.35407°N, 9.31507°E):
Meggerdorf
Schleswig_HOLSTEIN
Allemagne
Ces deux points sont faciles à visualiser sur Google Earth.
Remarque:
En plus du méridien de Paris, il faut aussi prendre en considération qu’en 1800, les cartes utilisées n’étaient pas référencées au système géodésique WGS84. Tout cela risque de rendre plus difficile la localisation exacte du point B.
Il s’agissait bien d’une boutade , mais comme dans le dernier commentaire vous mentionniez:
« Dans ce cas, aucune chance de trouver un trésor enfoui au point B en 1800! ».
Du coup, mon imagination s’est mise en branle dans un exercice d’improvisation avec un général français magouilleur et son trésor rapporté d’Égypte.
En fait, au départ, j’avais choisit un point A (50°30’30″N et 5°30’30″ E) au hasard en pensant qu’il devait se trouver quelque part en France compte tenu de la longitude et de la latitude.
En vérifiant sur Google Earth et en utilisant en plus le méridien de Paris comme degré 0 de longitude, mon point A est en fait en Allemagne quelque part en Rhénanie et c’est une autre histoire à imaginer…
Enfin, tous ces exercices m’ont permis de me familiariser un peu avec l’importance de la déclinaison magnétique, ce qui était le but.
merci.
Pourquoi faire simple quand on peut faire compliqué…
Je pense même que tu n’avais pas besoin d’aide pour comprendre la déclinaison magnétique et effectuer les calculs d’application.
Bonjour Bernard,
J’ai intégré il y a bien longtemps l’écart entre le Nord magnétique et le Nord géographique, et ce avant les cartes reliées aux GPS, lors d’une traversée de l’Atlantique (on disait alors qu’au cap déterminé à la table à carte, il fallait ajouter des degrés pour indiquer le cap vrai au barreur sur le compas ; le moyen mnémotechnique étant qu’on s’habillait en quittant la table à carte pour sortir du carré vers l’extérieur, donc qu’on ajoutait des vêtements, donc des degrés pour le cap vrai. Ce raisonnement était vrai disait-on pour l’hémisphère nord) (je sais pas si j’ai été très simple, là:).
Mais les maths ont toujours été une souffrance pour moi (il fallait calculer les fameuses minutes) et quand on ne navigue pas régulièrement, on perd la théorie.
Bref, j’ai acheté une montre (Casio pour la nommer) avec une boussole numérique censé m’indiquer le nord magnétique. Ce qu’elle ne fait pas du tout (j’ai un compas à côté en comparaison). J’ai tenté de la régler deux fois sans succès.
Sais-tu quelle est la fiabilité de ce type d’appareils ? Cette montre serait bien utile en voyage et m’éviterait d’emmener avec moi mon compas. Si je ne peux m’y fier et que ce n’est qu’un gadget inefficace, elle repartira à l’envoyeur.
Pour info, mon Iphone m’indique le nord magnétique avec une erreur de près de 20°, ce qui est énorme.
Existe t-il des boussoles numériques fiables ?
Merci de tes réponses,
Guillaume
Bonjour Guillaume,
Les boussoles numériques sont effectivement plus ou moins précises. Pour ce qui de l’orientation, je conseille d’ailleurs toujours une boussole mécanique, fiable et plus facile à utiliser avec une carte.
Sur ma Suunto Vector j’ai un petit décalage mais inférieur à 5° environ, après je ne m’en sers jamais pour des manipulations précises, je privilégie une boussole à plaquette.
Sur un de mes GPS, la boussole est très précise que ce soit à l’arrêt ou en mouvement (calcul fait de manière différente).
Donc pour répondre à ta question : oui. Mais il faut les trouver et je ne sais pas si ça l’est dans le temps.
A bientôt,
François
Bonjour Guillaume,
Vous ne dites pas si vous faites la calibration de la boussole numérique (à chaque démarrage à froid)
ça peut avoir de l’importance …
ces boussoles électroniques amplifient le signal d’un capteur de champ, (je dirais amplifient trop), il faut distinguer le champ terrestre des champs parasites, ce que la procédure de calibration donnée par le fabricant est censée faire.
j’ai déjà évoqué la chose plus haut.
https://www.randonner-malin.com/la-declinaison-magnetique/#comment-52228
cordialement.
Ils existe 3 nord, vous avez oubliez le « grid north », nord quadrillage.
Il est pourtant mentionné dans l’article…
Je suppose qu’il y-a déjà beaucoup de commentaires qui t’encourage mais cela ne m’empêche de féliciter la qualité des écrits c’est simple et compréhensible.
Merci bien
Merci pour vos explications précises et limpides !
Merci François pour les explications.
Bravo François, succès bien mérité pour ton site !
Question svp à qui veut bien me répondre, car je m’emmêle les pinceaux :
Je reprends ton exemple : me trouvant en un point du globe où la déclinaison est de 20°O, j’ai fait le réglage de ma boussole en conséquence, avec un Nord magnétique de l’aiguille bien distinctement à gauche du Nord géographique du cadran.
1) Comment placer la boussole sur la carte ? Toujours en alignant les bords de celle-ci sur le N géographique de la carte, ou au contraire en alignant l’aiguille sur le N géographique de la carte ?
2) Après cela, comment déterminer un azimut donné (dans ton exemple : point B = 90°E par rapport au point A) ? A partir du N indiqué par l’aiguille de ma boussole, ou du N indiqué par le cadran de ma boussole ?
J’imagine que la réponse est plus simple que ma question, mais encore une fois je suis un peu
« emmêlé ». Merci d’avance !
1) Tout dépend de la méthode de correction que tu utilises. Ce qu’il faut est être dans le même monde sur la carte et sur le terrain et utiliser la même référence. Tu peux utiliser soit le nord magnétique soit le nord géographique. Dasn le premier cas, tu corriges sur la carte et dans le second sur la boussole.
2) Cela dépend quelle référence tu utilises.
Merci François pour tes explications. Mais … Tu écris: « Le nord géographique correspond la plupart du temps au haut des cartes topographiques. C’est le cas pour les cartes de l’IGN ».
Malheureusement, ce n’est pas (ou plus) vrai. Je ne connais jusqu’à présent que des cartes d’Allemagne, d’Autriche, d’Angleterre, où c’est effectivement le cas. Le bord supérieur de la carte indique le nord géographique. De même que le bord de la carte. Et les noms de lieux se situent sur la ligne géographique ouest-est. C’est la convention depuis des lustres.
Sur les cartes de l’IGN, l’ensemble du système de coordonnées UTM est incliné par rapport à la zone cartographique. Il n’y a plus de lignes verticales. Le seul vertical est le bord de la carte, mais il n’indique pas le nord géographique ! Et cela signifie que les noms de lieux ne pointent plus vers l’ouest ou l’est. Mais il n’est indiqué nulle part. Incroyable…. Et puis l’IGN a le culot de nous dire sur son site que nous devrions utiliser la ligne noire du méridien pour déterminer l’azimut. Il y a une ligne de méridien tous les 25 centimètres. On ne peut pas travailler avec ça. C’est un cauchemar. Suis-je censé utiliser une règle pour établir les parallèles sur la carte avant la visite ?! Amusez-vous bien. Les cartographes de l’IGN ne se soucient manifestement plus des utilisateurs de boussoles, mais seulement des randonneurs GPS. Mais ils n’ont pas vraiment besoin de cartes….
Tu as tout à fait raison, dans les éditions récentes les bords de la carte ne sont plus alignés en direction du nord géographique – et c’est bien dommage. Les seules indications pour connaitre la direction du nord géographique sont effectivement les méridiens et les amorces de méridiens.
Pour relever ou reporter des azimuts, ça vaut effectivement le coup de tracer quelques méridiens supplémentaires.
Bonjour,
Votre définition de la déclinaison magnétique n’est pas tout à fait correcte.
Il ne s’agit en effet pas de l’écart entre Nord géographique et Nord magnétique, mais de l’écart entre Nord Vrai et Nord magnétique.
Voir à ce sujet un site canadien très bien conçu :
https://www.geomag.nrcan.gc.ca/mag_fld/magdec-fr.php
Cordialement
Le « nord vrai » et le « nord géographique » sont la même chose, c’est d’ailleurs indiqué dans l’article que vous avez mis dans votre commentaire.
ancien militaire et topographe , on rajoute un 3eme nord , le nord du quadrillage de la carte . pour decliner une boussole precisement un peu comme avec un theodolite . il faut trouver une borne et avoir un carnet de pts ou une carte ratm . s’installer sur une borne et prendre 4 visees sur des pts precis dont on a les gisements dans 4 quadrants differents ( 0 à 1600 , 1600 à 3200 , 3200 à 4800 et 4800 à 6400 ) . on travaille en milliemes otan (le tour à 6400 ) . les russes sont sur 6000. on fait une moyenne avec 4 visees boussole et on peut decliner sa boussole en ecrivant dessus pour une mk1 par exemple la correction . par exemple -4 mil . donc , quand on fera une visée (azimut ) on deduira 4 pour avoir le gisement .on peut egalement le faire plus simplement mais moins precisement en partant sur les coord d’un carrefour par exemple , calculez au rapporteur le gisement sur une carte au 1/25000 ou au 1/50000 d’etat major . prendre la visée boussole (azimut ) et calculer la difference qui il est vrai est faible (autour de 4 chez moi dans l’est du cantal ) . quand je suis entré à l’armee en 68 elle etait environ de 130 mil
.
avec une calculatrice du style ancienne hp 31 , on peut calculer le gisement distance entre 2 pts du terrain avec une fiche adequat en entrant les coord. ensuite faire d’un pt vers l’autre la visée boussole (azm ) et deduire la difference .
petite precision , les coord . employées au niveau de l’armée de terre sont en systeme UTM .
la definition du millieme est approx. l’angle sous lequel on voit un metre à un km . 1degré = 17.7777 mil .8 mil = 27 min .en artillerie et mortier d’infanterie nous utilisions des theodolites , gyro et boussole de type anglaise mk 1 pour la topo et la mise en direction des pices de tir. En 78 au tchad , pendant l’operation tacaud , en tant qu’officier de tir de la section de mortier lourd du 3 rima de vannes à moussoro , j’ai eu l’occasion de faire tirer les orgues de staline (bm 15 katioucha russe ) de l’armée locale dont les appareils de pointage etaient evidemment en mil russe (6000) , donc avec nos appareils topo , mk1 et thedolite nous leurs calculions les elements de tir en mil .otan (6400) , d’ou l’obligation d’avoir une bonne calculette !!!! lol
Bonjour pour le temps que vous avez consacré a vos explications et vos réponses aux questions.
il y a je pense une incompréhension de ma part
au tout début vous avez mis deux schéma de déclinaison E et W ( E+ et W-)
dans votre exemple des solution de correction vous avez pris un exemple d’une déclinaison de 20° et la flèche est orienté vers W- ( Pourquoi vous n’avez pas mis -20 ??
donc si j’ai un azimute 100° je dois faire 100 – (-20) ce qui fait 120° donc l’azimute à suivre est de 120°
Maintenant imaginons que j’ai une déclinaison positive Est de 20°
prenant le même exemple avec l’azimute de 100°
je dois faire 100 – 20 = 80° donc l’azimute à suivre et de 80°?
Merci à toi
Bonjour, je viens juste de trouver votre site qui est très intéressant. Merci.
J’ai une question concernant la déclinaison:
J’ai une carte topo de 1:50000 année de 1973 avec changement annuel de2.7, si je fais la différence avec 2022 ça fait 49 ans fois 2.7, = 132.3′, divisé par 60′ = 2 degré et 13′ Donc 23degré 25′ moins 2 degré 12′ donne 2 degré 12 ‘ donc la déclinaison d’aujourd’hui devrait donc être de 21degré .13’
Sur votre site la déclinaison est de 16degré W est-ce que vous pouvez m’expliquer la différence ?
Merci
Ben
20 Evangeline St-Quentin, NB E8A 1M7 tel: 506-235-2532
Le changement annuel est une estimation et il n’est pas constant chaque année. Sur de grandes périodes comme dans votre exemple (49 ans), on peut avoir des différences non négligeables. Il vaut donc mieux se fier au site dans ce cas.
Ouf…en France nous pouvons négliger la déclinaison magnétique….
Depuis que j’ai fait 12 km dans le mauvais sens… je me suis achetée une boussole Silva sans loupe, mon ami m’ a lui offert une Silva avec miroir…qui reste encore un grand mystère. La loupe est-elle un plus indispensable?
Merci. J’espère que la vieille dame que je suis, va comprendre tout ce que vous m’expliquez.
Cordialement. Chtal
La loupe peut aider, mais elles ne sont pas toujours très pratiques sur les boussoles car petites. Donc ça peut valoir le coup d’avoir une loupe séparée.